Momen quán tính là gì? Công thức tính trong các trường hợp khác nhau

Chu Văn An

Nội dung bài viết

Momen quán tính là đại lượng đặc trưng cho khả năng của vật chống lại sự thay đổi vận tốc góc. Giá trị này bị ảnh hưởng bởi nhiều yếu tố khác nhau nên công thức tính trong các trường hợp khác nhau cũng khác nhau. Hãy cùng tìm hiểu trong bài viết dưới đây

1. Mô men quán tính là gì?

Mômen quán tính là một đại lượng vật lý đặc trưng cho khả năng của vật chống lại sự thay đổi vận tốc góc trong chuyển động quay, tương tự như khối lượng trong chuyển động thẳng. Nói một cách đơn giản, nó thể hiện khả năng chống lại sự thay đổi vận tốc góc của cơ thể, giống như khối lượng thể hiện khả năng chống lại sự thay đổi vận tốc trong chuyển động không quay (tuyến tính), theo định luật chuyển động của Newton.

Sự phân bố khối lượng trong vật và vị trí của trục quay quyết định mô men quán tính. Do đó, dù vật là như nhau nhưng các giá trị quán tính có thể rất khác nhau, tùy thuộc vào vị trí và hướng của trục quay.

2. Công thức tính mô men quán tính

Dựa vào khái niệm mô men quán tính, người ta có thể đưa ra công thức tổng quát để tính giá trị của đại lượng này như sau:

Tôi = ông2

Trong đó:

M là khối lượng của vật

R là khoảng cách từ vật tới trục quay

Cách tính mômen quán tính bằng tích phân

Tương đối dễ dàng sử dụng công thức chung cho các đối tượng được coi là tập hợp các điểm riêng biệt. Tuy nhiên, công thức này gần như không thể áp dụng nếu bạn muốn tính toán cho những đối tượng phức tạp hơn. Sau đó, bạn cần sử dụng công thức tích phân cho toàn bộ tập. Giá trị của độ lớn mômen lực là hàm mật độ khối lượng tại mỗi điểm r. Trong đó r là vectơ bán kính tính từ các điểm đến trục quay.

Xem thêm Hóa chất Polimer trong xử lý nước thải ra sao ?

maxresdefault

3. Momen quán tính của bề mặt hình trụ tròn hoặc hình trụ rỗng

Chúng ta có thể chia đường tròn thành k cung bằng nhau. Khi k tiến đến vô cùng, chúng ta coi mỗi cung là một điểm, kết quả cuối cùng là

Tôi = mR2

4. Momen quán tính của hình trụ đặc hoặc đĩa tròn mỏng

van

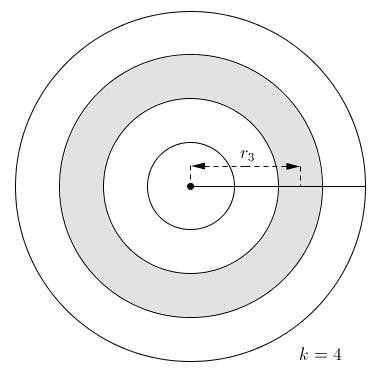
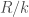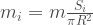Chúng ta sẽ chia đĩa thành k lớp, mỗi lớp dày R/k diện tích của lớp thứ i tính từ tâm là $S_i = \pi[(\frac{iR}{k})^2-(\frac{(i-1)R}{k})^2]$ do đó khối lượng của lớp thứ i tính từ tâm đĩa sẽ là $m_i=m\frac{S_i}{\pi R^2}$ khoảng cách từ tâm đến trung vị của lớp là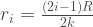 $r_i = \frac{(2i-1)R}{2k}$

Mômen quán tính của đĩa bằng tổng mômen quán tính của các lớp tạo nên nó (các lớp này có thể được coi là các vòng tròn khi k tiến đến vô cùng).

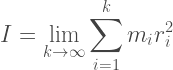
$\displaystyle I=\lim_{k \to \infty} \sum_{i=1}^k m_ir_i^2$

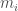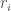Thay thế giá trị m_i Và r_i tính toán ở trên và đơn giản hóa, chúng tôi nhận được

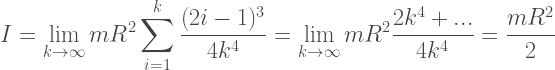
${\displaystyle~I=\lim_{k\to\infty}mR^2\sum_{i=1}^k\frac{(2i-1)^3}{4k^4}=\lim_{k\to \infty}mR^2\frac{2k^4+...}{4k^4}=\frac{mR^2}{2}}$

5. Momen quán tính của quả cầu (quả cầu rỗng)

Chúng ta sẽ tính mô men quán tính của nửa hình cầu. Dùng k-1 mặt phẳng vuông góc với trục quay, chia bán kính trùng với trục quay thành k phần bằng nhau. Các mặt phẳng k-1 này cắt nửa hình cầu tại k-1 đường tròn, chia nửa hình cầu thành k phần bằng nhau. diện tích bằng nhau và bằng nhau 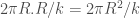$2\pi R. R/k=2\pi R^2/k$ vậy mỗi phần có khối lượng 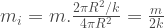$m_i= m. \frac{2\pi R^2/k}{4\pi R^2}=\frac{m}{2k}$ mặt khác, khoảng cách từ trục quay đến đường trung bình của phần thứ i tính từ tâm là $r_i= \sqrt{R^2 - (\frac{(2i-1)R}{2k})^2}$

Momen quán tính của nửa hình cầu bằng tổng mômen quán tính của k vòng tạo nên nó

Xem thêm Vinyl axetat là gì? Tính chất và Ứng dụng trong sản xuất

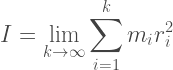
$\displaystyle I=\lim_{k \to \infty} \sum_{i=1}^k m_ir_i^2$

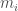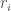Thay thế giá trị m_i Và r_i tính toán ở trên và đơn giản hóa, chúng tôi nhận được

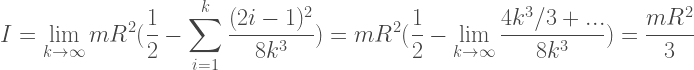
${\displaystyle~I=\lim_{k\to\infty}mR^2(\frac{1}{2}-\sum_{i=1}^k\frac{(2i-1)^2}{8 k^3})=mR^2(\frac{1}{2}-\lim_{k\to\infty}\frac{4k^3/3+...}{8k^3})=\frac {mR^2}{3}}$

Vậy mô men quán tính của toàn bộ quả cầu là

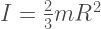
$I=\frac{2}{3}mR^2$

6. Momen quán tính của quả cầu rắn

Đối với vật rắn hình cầu quay có thành dày, công thức xác định mô men quán tính sẽ là:

Tôi = (2/3).m.r2

Trong đó, m là khối lượng của vật rắn và r là bán kính của hình cầu

7. Momen quán tính của hình trụ rỗng

Công thức mô men quán tính của một hình trụ rỗng khối lượng M có trục quay trên một trục đi qua tâm hình trụ có bán kính trong R1 và bán kính ngoài R2 được xác định như sau:

Tôi = (1/2). M.(R12 + R22)

8. Vật hình chữ nhật có trục quay hướng tâm

Đối với các vật hình chữ nhật mỏng, quay trên một trục vuông góc với tâm của tấm. Độ lớn mômen quán tính được xác định theo công thức:

Tôi = (1/12)m(a2+b2)

Trong đó:

M là khối lượng của vật
A là chiều dài hình chữ nhật
B là chiều rộng của hình chữ nhật

9. Các lý thuyết liên quan

Định lý Huygen: Mômen quán tính đối với trục ban đầu bằng mômen quán tính đối với trục đi qua tâm song song với trục đó, cộng với tích của khối lượng của vật và bình phương khoảng cách giữa hai trục.

Io = I1 + m.d2 .Io = I1 + m.d2

Io: Momen quán tính đối với trục ban đầu

I1: Momen quán tính đối với trục mới

m: Khối lượng của vật

d: khoảng cách giữa hai trục

Tính hai đại lượng chính trong chuyển động quay (điều kiện: mô men quán tính của một vật quay quanh một vật cố định)

Xem thêm Pipet thẳng là gì? Cách sử dụng ống nhỏ giọt đơn giản, dễ thực hiện

Động năng quay: K = lw2

Động lượng góc: L = lw

Trên đây là toàn bộ thông tin về mô men quán tính và công thức tính giá trị trong các trường hợp khác nhau. Đừng quên theo dõi Vietchem để cập nhật những nội dung thú vị khác

Hóa Chất