Nội dung bài viết
To accurately determine the wire cross-section, it is necessary to calculate the load the wire must bear. You can follow the detailed wire load calculation formula in our following article.
Why is it necessary to calculate wire load?
Electrical wire load is the load-carrying capacity of electrical wires in a system or line. This is the maximum electrical capacity that the conductor can carry safely and continuously without overloading or overheating.

The wire load is proportional to the wire cross-section. The higher the load, the larger the wire cross-section. The copper core usually carries the load better than the aluminum core.
Accurate calculation of wire load plays an important role in:
- Ensuring electrical safety: Avoid situations where the power cord is overloaded, overheated, or has the wire melting, causing the risk of fire or electric shock.
- Reduce power loss: Wires with too small cross-sections can easily cause voltage drops, reduce device performance, and waste electricity.
- Increase device life: Conductors suitable for the load help the device operate stably and maintain a long life.
Formula for calculating electric wire load
To calculate the electric wire load, it is first necessary to determine two input quantities: power consumption and current intensity of the device in an area or line.
The formula for calculating electric wire capacity is as follows:
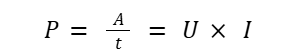
In there:
- P: Power consumption (W)
- A: Power consumption (J)
- t: Time of electricity use
- U: Voltage (V)
- I: Current intensity (A)
Converting to W unit of power consumption: we have: 1kW = 1,000W, 1mW = 1,000,000W
After having the value of power consumption, the formula for calculating current intensity is:
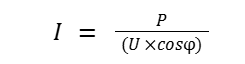
In there:
- P: Power consumption (W)
- I: Current intensity (A)
- U: Voltage (V)
- Cosφ: Power factor, usually 0.8.
For 3-phase power systems, the formula for calculating current intensity is applied:
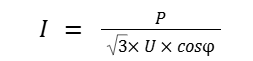
Finally, the wire cross section is also the value that determines the wire load calculated through the formula:
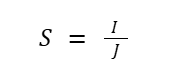
In there:
- J: Allowable current density (A/mm2), for copper wire is usually 6A/mm2, for aluminum wire is 4.5A/mm2
- I: Current intensity (A)
Electric wire selection table according to capacity

With power cable
| Cable cross section | Load capacity | |
| PVC insulation | XLPE insulation | |
| mm2 | ≤kW | kW |
| 3 | 6.4 | 8.2 |
| 4 | 7.6 | 9.8 |
| 5 | 8.8 | 11.2 |
| 5.5 | 9.4 | 11.9 |
| 6 | 9.8 | 12.4 |
| 7 | 10.8 | 13.8 |
| 8 | 11.8 | 15 |
| 10 | 13.4 | 17 |
| 11 | 14.2 | 18.1 |
| 14 | 16.6 | 20.7 |
| 16 | 17.8 | 22 |
| 22 | 22 | 27.2 |
| 25 | 23.6 | 29.2 |
| 35 | 29 | 36 |
With VC, CV, CVV wires
| Wire cross section (mm2) | Load capacity (≤kW) |
| 0.5 | 0.8 |
| 0.75 | 1.3 |
| 1 | 1.8 |
| 1.25 | 2.1 |
| 1.5 | 2.6 |
| 2 | 3.6 |
| 2.5 | 4.4 |
| 3 | 5.6 |
| 4 | 7.3 |
| 5 | 8.7 |
| 6 | 10.3 |
| 7 | 11.4 |
| 8 | 12.5 |
| 10 | 14.3 |
Table to look up the allowable current of the conductor
The wire current lookup table is often applied to electrical wires buried underground.
For directly buried electric cables
Main parameters:
- Thermal resistivity of soil: 1.20Cm/W
- Average soil temperature: 150 degrees Celsius
- Underground wire burial depth: 0.5m
- Maximum operating temperature of the conductive core: 700 degrees Celsius.
Because the rated current of underground cables depends on soil temperature and soil thermal resistivity, when choosing cables, it is necessary to consider both the correction coefficient of the conductor, the grouping coefficient, as well as the voltage drop of cable types such as CVV/DTA, CVV/WA.
Follow the table below to check the allowable current of directly buried cables:
| Conductor cross-section | 1 core | 2 cores | 3 and 4 cores | |||||
| 2 cables placed at distance | The 3 cables contact each other in a 3-leaf shape | |||||||
| Rated current | Pressure drop | Rated current | Pressure drop | Rated current | Pressure drop | Rated current | Pressure drop | |
| mm2 | A | mV | A | mV | A | mV | A | mV |
| 1.5 | 33 | 32 | 29 | 25 | 32 | 29 | 27 | 25 |
| 2.5 | 44 | 20 | 38 | 15 | 41 | 17 | 35 | 15 |
| 4 | 59 | 11 | 53 | 9.5 | 55 | 11 | 47 | 9.5 |
| 6 | 75 | 9 | 66 | 6.4 | 69 | 7.4 | 59 | 6.4 |
| 10 | 101 | 4.8 | 86 | 3.8 | 92 | 4.4 | 78 | 3.8 |
| 16 | 128 | 3.2 | 110 | 2.4 | 119 | 2.8 | 101 | 2.4 |
| 25 | 168 | 1.9 | 142 | 1.5 | 158 | 1.7 | 132 | 1.5 |
| 35 | 201 | 1.4 | 170 | 1.1 | 190 | 1.3 | 159 | 1.1 |
| 50 | 238 | 0.97 | 203 | 0.82 | 225 | 0.94 | 188 | 0.82 |
| 70 | 292 | 0.67 | 248 | 0.58 | 277 | 0.66 | 233 | 0.57 |
| 95 | 349 | 0.50 | 297 | 0.44 | 332 | 0.49 | 279 | 0.42 |
| 120 | 396 | 0.42 | 337 | 0.36 | 377 | 0.40 | 317 | 0.35 |
| 150 | 443 | 0.36 | 376 | 0.31 | 422 | 0.34 | 355 | 0.29 |
| 185 | 497 | 0.31 | 423 | 0.27 | 478 | 0.29 | 401 | 0.25 |
| 240 | 571 | 0.26 | 485 | 0.23 | 561 | 0.24 | 462 | 0.21 |
| 300 | 640 | 0.23 | 542 | 0.20 | 616 | 0.21 | 517 | 0.18 |
| 400 | 708 | 0.22 | 600 | 0.19 | 693 | 0.19 | 580 | 0.17 |
| 500 | 780 | 0.20 | 660 | 0.18 | – | – | – | – |
| 630 | 856 | 0.19 | 721 | 0.16 | – | – | – | – |
| 800 | 895 | 0.18 | 756 | 0.16 | – | – | – | – |
| 1000 | 939 | 0.18 | 797 | 0.15 | – | – | – | |
For underground cables installed in single-line pipes
Main parameters:
- Thermal resistivity of soil: 1.20Cm/W
- Soil temperature: 150 degrees Celsius
- Cable burial depth: 0.5m
- Maximum working temperature of the conductive core: 700 degrees Celsius
Conductor current table:
| 2 cables: tubes contact each other | 3 cables: tubes arranged in a three-leaf shape touching each other | |||||||
| Section | Rated current | Pressure drop | Rated current | Conductor cross-section | 1 core | 2 cores | 3 and 4 cores | Pressure drop |
| mm2 | A | mV | A | mV | A | mV | A | mV |
| 1.5 | 30 | 34 | 28 | 27 | 26 | 29 | 22 | 25 |
| 2.5 | 41 | 22 | 35 | 16 | 34 | 17 | 29 | 15 |
| 4 | 59 | 12 | 48 | 10.5 | 45 | 11 | 38 | 9.5 |
| 6 | 69 | 10 | 60 | 7.0 | 57 | 7.4 | 48 | 6.4 |
| 10 | 90 | 5.0 | 84 | 4.0 | 76 | 4.4 | 64 | 3.8 |
| 16 | 114 | 3.4 | 107 | 2.6 | 98 | 2.8 | 83 | 2.4 |
| 25 | 150 | 2.0 | 139 | 1.6 | 129 | 1.7 | 107 | 1.5 |
| 35 | 175 | 1.4 | 168 | 1.2 | 154 | 1.3 | 129 | 1.1 |
| 50 | 216 | 1.0 | 199 | 0.88 | 183 | 0.94 | 153 | 0.82 |
| 70 | 262 | 0.76 | 241 | 0.66 | 225 | 0.66 | 190 | 0.57 |
| 95 | 308 | 0.61 | 282 | 0.53 | 271 | 0.49 | 228 | 0.42 |
| 120 | 341 | 0.54 | 311 | 0.47 | 309 | 0.40 | 260 | 0.35 |
| 150 | 375 | 0.48 | 342 | 0.42 | 346 | 0.34 | 292 | 0.29 |
| 185 | 414 | 0.44 | 375 | 0.38 | 393 | 0.29 | 331 | 0.25 |
| 240 | 463 | 0.40 | 419 | 0.34 | 455 | 0.24 | 382 | 0.21 |
| 300 | 509 | 0.37 | 459 | 0.32 | 510 | 0.21 | 428 | 0.18 |
| 400 | 545 | 0.34 | 489 | 0.30 | 574 | 0.19 | 490 | 0.17 |
| 500 | 585 | 0.32 | 523 | 0.28 | – | – | – | – |
| 630 | 632 | 0.30 | 563 | 0.26 | – | – | – | – |
| 800 | 662 | 0.28 | 587 | 0.25 | – | – | – | – |
| 1000 | 703 | 0.27 | 621 | 0.23 | – | – | – | – |
In addition, you can also look up the cross-sectional area according to the rated current of PVC and XLPE insulated wires according to the following table.
| Conductor cross section | PVC sheathed power wire | PVC sheathed power wire | XLPE sheathed power wire | XLPE sheathed power wire |
| CV | AV | CX | AX | |
| mm2 | Ampere | Ampere | Ampere | Ampere |
| 1.0 mm2 | – | – | 20 A | – |
| 1.5mm2 | 20 A | – | 26 A | – |
| 2.5 mm2 | 27 A | – | 36 A | – |
| 4.0 mm2 | 37 A | – | 49 A | – |
| 6.0 mm2 | 47 A | – | 63 A | – |
| 10mm2 | 65 A | 52 A | 86 A | 68 A |
| 16mm2 | 87 A | 70A | 115 A | 92 A |
| 25mm2 | 114 A | 91 A | 149 A | 119 A |
| 35 mm2 | 140 A | 112 A | 185 A | 148 A |
| 50mm2 | 189 A | 151 A | 225 A | 180 A |
| 70mm2 | 215 A | 172 A | 289 A | 230 A |
| 95mm2 | 260 A | 208 A | 352 A | 281 A |
| 120mm2 | 324 A | 259 A | 420 A | 328 A |
| 150 mm2 | 384 A | 307 A | 473 A | 378 A |
| 185 mm2 | 405A | 324 A | 542 A | 430 A |
| 240 mm2 | 518 A | 414 A | 641 A | 512 A |
| 300 mm2 | 570 A | 456 A | 741 A | 592 A |
| 400 mm2 | 660 A | 528 A | 830 A | – |
| 500 mm2 | 792 A | 633 A | 905A | – |
| 630 mm2 | 904 A | 723 A | 1019 A | – |
| 800 mm2 | 1030A | 824 A | 1202 A | – |
Example of wire load calculation
To better understand how to calculate wire loads, you can follow some examples of choosing wire cross-sections for large capacity devices in 1-phase and 3-phase power systems below.
How to calculate electrical wire load for air conditioner
Air conditioners are high-capacity devices in the home electrical system, so it is necessary to ensure that the wires have the appropriate load-bearing capacity, especially when the machine starts, the wires will have to endure a sudden increase in starting current.
We have: 1 HP 9000BTU air conditioner, power consumption 0.7456kW, using 220V/50Hz power source.
Conversion: 0.7456kW = 745.6W
Applying the formula, we can calculate the current intensity the conditioner must endure:
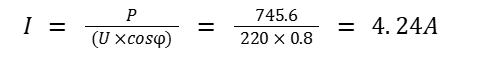
From there, the conductor cross-section for the harmonic copper wire can be calculated:
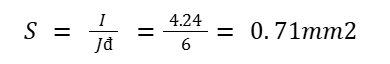
Manufacturers recommend choosing a wire cross section 1 level larger than the calculated value to ensure load-carrying capacity and conveniently expand the load later.
Choose a wire with a cross section of 1 – 1.5mm2 for a 1HP air conditioner.
How to calculate electrical wire load for refrigerators
Example 1: 300W refrigerator, used voltage 220V/50Hz.
Applying the same formulas as above, we can calculate the current intensity and corresponding wire cross-section:
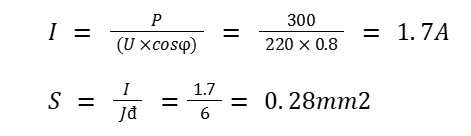
With the above results, you can choose a wire with the smallest cross-section of 0.75mm2 or 1mm2 for a 300W refrigerator. However, to avoid voltage drop, the market often uses double electrical wires for refrigerators with a cross section of 1.5mm2.
Choose a wire with a cross section of 2 x 1mm2 or 2 x 1.5mm2 for a 330W refrigerator.
Example 2: How many watts of load can a 2.5 mm2 electrical wire for a refrigerator withstand?
The electrical wire used for family refrigerators is usually copper core, operating at 220V voltage.
Applying the formula, we can calculate the current intensity of a 2.5mm2 wire used for the refrigerator:
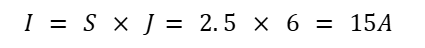
Correspondingly, a 2.5mm2 wire can withstand a maximum capacity of:
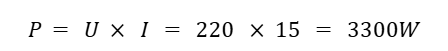
How to calculate electrical wire load for water heater
We have: 4500W water heater, operating voltage 220V/50Hz.
Apply the following formula to calculate current intensity and wire cross-section:
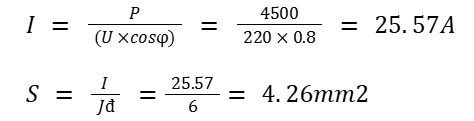
On the market, electric wires with a cross section of 4mm2 can carry a load of up to 7000W, so you can choose a wire with a cross section of 4mm2 in this case.
Choose a wire with a cross section of 2 x 4mm2 for a 4500W water heater.
How to calculate wire load for electric motor
We have: A 3-phase electric motor with capacity of 15kW, voltage of 380V.
Conversion: 15kW = 15000W. The cosφ coefficient of electric motors is usually 0.85 larger than that of civil equipment.
Apply the load calculation formula:
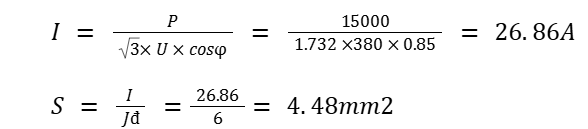
Choose a wire with a cross section of 6mm2 for a 15kW electric motor.
Some questions about calculating wire loads
Question 1: Can conductors with cross-sections smaller than the calculated value be used?
Reply: In fact, you should choose an electric wire with a cross-section greater than or equal to the calculated value to create a safety factor, minimizing overload and line voltage drop. However, it is still possible to choose a wire cross section smaller than the calculated value if the device capacity has not exceeded the recommended power value corresponding to the wire cross section in the wire cross section table according to capacity.
Question 2: Can all systems and equipment use the same method of calculating wire load as above?
Reply: In theory yes. However, the formula for calculating current intensity is different between 1-phase and 3-phase electricity. At the same time, if you need to calculate the wire load for the entire electrical system, you need to calculate the total capacity of all devices used at the same time.
Other knowledge related to electrical wire loading, you can learn at: https://etinco.vn/tin-tuc/kien-thuc/kien-thuc-day-cap-dien/.


Nội dung được phát triển bởi đội ngũ truongchuvananhue.edu.vn với mục đích chia sẻ và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 0000 hoặc email: hotro@truongchuvananhue.edu.vn